(с) 2005 (интернет-публикация) СНК "Пульс Будущего".
При использовании данного материала ссылка обязательна.
http://pulse.webservis.ru/Science/Ether/LostLink
(с) 2004 З.К. Нуриев, (с) 2004 ГАГУ, (с) 2005 (интернет-публикация) СНК "Пульс Будущего". При использовании данного материала ссылка обязательна. http://pulse.webservis.ru/Science/Ether/LostLink |
Фундаментальные законы классической физики, закон Кулона, описывающий силу (назовем ее пока F1) взаимодействия двух заряженных частиц в зависимости от квадрата расстояния между ними и закон всемирного тяготения, описывающий силу притяжения (назовем ее F3) двух масс от квадрата расстояния между ними широко известны. Известен также в электромагнетизме закон Ампера, описывающий силу (назовем ее F2) взаимодействия двух расположенных параллельно друг другу проводников с протекающими в них токами от длины этих проводников и расстояния между ними. То есть имеется два рода поля, электрическое и магнитное в электромагнетизме и только одно гравитационное в механике. С одной стороны пара сил, с другой — одна сила. Тогда, учитывая принцип симметричности и великого равновесия, в котором пребывает окружающий нас мир, неизбежно напрашивается вполне банальный вопрос — а где же четвертая сила (F4)? Природу какого поля она описывает и с какой универсальной постоянной взаимодействует? Диэлектрическая проницаемость вакуума ε0 устанавливает соответствие в законе Кулона с принятой в классической физике системой единиц, магнитная проницаемость вакуума μ0 приводит в соответствие силовое взаимодействие токов в законе Ампера с принятой системой единиц и, наконец, гравитационная постоянная g0 (или постоянная тяготения) также является коэффициентом пропорциональности в гравитационном законе Ньютона. И, по всей вероятности, система фундаментальных уравнений должна выглядеть следующим образом:
электромагнетизм | ||
| где | (1) | |
| где | (2) | |
механика | ||
где 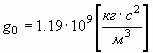 , , | (3) | |
| F4= ?, | ————— | (4) |
Закон Ньютона здесь записан в виде, аналогичном закону Кулона с приведенным к данному виду значением гравитационной постоянной g0.
Нет никакого сомнения в том, что предпринималось немало попыток объяснить физическую природу этой четвертой силы и определить численное значение и размерность коэффициента пропорциональности и, тем самым, завершить этот квадрант. В книге В.Л.Дятлова [2], например, в его поляризационной модели неоднородного физического вакуума, в сравнительной таблице уравнений Хевисайда и Максвела даже приводится эта четвертая универсальная постоянная под названием спиновая постоянная ε0 или спиновая проницаемость вакуума, равная:
| s0 = 0.9329 · 10-26 [м·кг]. | (5) |
Численное значение и размерность спиновой постоянной были получены из условия, что произведение спиновой проницаемости вакуума на гравитационную постоянную вакуума обратно-пропорционально квадрату скорости распространения грависпиновых волн в вакууме, аналогично тому, как произведение диэлектрической проницаемости вакуума на магнитную проницаемость вакуума обратно-пропорционально квадрату скорости распространения электромагнитных волн в вакууме, или скорости света. Автор исходил из предположения, что скорость распространения грависпиновых волн, как и скорость распространения электромагнитных волн, равна скорости света.
Тем не менее, уравнения, описывающего природу и суть силы F4, в аналогичном, предыдущем трем уравнениям виде, в классической физике в настоящее время не существует или, по крайней мере, автору на глаза пока не попадалось. Кроме того, не существует никаких сколько-нибудь убедительных доказательств, что такого уравнения не может быть в принципе.
Со времен установления основных фундаментальных законов в классической физике была обнаружена система закономерностей между уравнениями и величинами в механике и электромагнетизме и выведена система сопоставлений между механической силой и электродвижущей силой (или напряжением), между массой и индуктивностью, между скоростью и током и т.д. Эти сопоставления довольно широко используются в настоящее время в математическом и аналоговом моделировании электромеханических систем.
Однако, если во всемирном законе тяготения и законе Кулона (6) проявляется такое удивительное сходство, то почему — бы не попытаться провести аналогию между
(6) |
массой m и зарядом q и продлить ее на весь дальнейший ход рассуждений. В любом учебнике физики можно увидеть графическую модель точечного электрического (положительного или отрицательного) заряда с расходящимися от него во все стороны (или сходящимися в нем) линиями электрического поля, и очень редко можно увидеть графическую модель массы с расходящимися от него радиально во все стороны (или сходящимися в нем, что принципиально, пока, значения не имеет) линиями гравитационного поля. Но, раз это поле существует, то должна существовать и напряженность гравитационного поля, подобно тому, как существует напряженность электрического поля Е. И, если напряженность электрического поля Е (рис. 1а) на расстоянии r от заряда (в вакууме) равна Е (7), то напряженность гравитационного поля (рис. 1б) равна G (8).
(7) | |
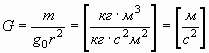 . . | (8) |
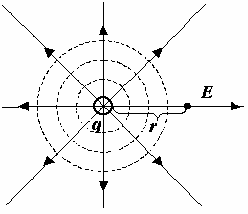 | 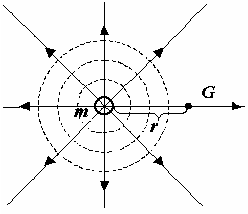 |
| а) заряд | б) масса |
| Рис. 1 | |
Небезынтересно отметить, что G имеет размерность ускорения (или ускорения свободного падения). Это значит, что наша планета, имеющая радиус около 6380 км и массу порядка 6·1024 кг, создает напряженность гравитационного поля на своей поверхности:
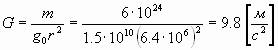 . . | (9) |
Т.е. ускорение свободного падения, вычисленное опытным путем, по сути дела и является напряженностью гравитационного поля Земли на его поверхности. И сила, с которой тело массы m притягивается к Земле, называемая в классической физике весом тела, равна произведению массы этого тела на напряженность гравитационного поля Земли:
(10) |
Произведение заряда на напряженность электрического поля также представляет собой силу:
(11) |
Далее, индукция электрического поля D определяется как:
(12) |
Следовательно, индукция гравитационного поля М, равна:
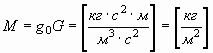 . . | (13) |
Здесь и далее в виду отсутствия в классической физике многих из рассматриваемых понятий, новые обозначения приводятся в произвольной форме, но при строгом соответствии размерностей, принятых в международной системе единиц. Электрические величины по мере возможности выражены через электрические единицы: Кл — кулон, в — вольт, а — ампер и т.д. Во многих учебниках размерность индуктивности, например, выражена в виде:
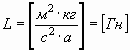 , , | (14) |
хотя это то же самое, что:
(15) |
Кроме того, учитывая, что количественная оценка рассматриваемых величин не производится, одноименные коэффициенты при универсальных постоянных отсутствуют.
Далее, из электротехники нам известно, что полный поток электрической индукции N через поверхность S есть сумма потоков электрической индукции через элементарные площадки, на которые может быть разбита поверхность S:
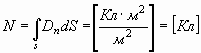 . . | (16) |
Т.е. для замкнутой поверхности, охватывающей заряд q, полный поток электрической индукции будет равен по величине самому заряду. Аналогично, полный поток гравитационной индукции О:
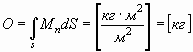 . . | (17) |
Т.е. для замкнутой сферы, охватывающей всю массу, полный поток гравитационной индукции будет равен самой массе.
Теперь перейдем к электрической емкости С. Известно, что емкость выражается как:
(18) |
и определяется через физические параметры как:
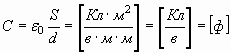 , , | (19) |
Т.к. в механике устройство, подобное конденсатору отсутствует, назовем его механической емкостью Z и выразим аналогично:
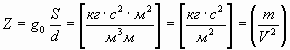 . . | (20) |
В круглых скобках указаны механические величины, в которых могут выражаться получаемые размерности. Отсюда можно предположить, что аналогом напряжения U является квадрат скорости V2:
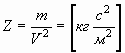 . . | (21) |
Кстати, также известно, что сила, с которой пластины конденсатора притягиваются друг к другу, равна:
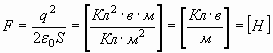 . . | (22) |
В "механической" емкости эта сила соответственно равна:
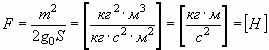 . . | (23) |
Не этим ли объясняется тот факт, что находящиеся в воде или смоченные изнутри, сведенные вместе два куска стекла, довольно трудно разъединить и чем больше площадь и масса стекол, тем сложнее это сделать. Ведь, в случае с конденсатором, при использовании между обкладками конденсатора высокопрочного диэлектрика, скажем, на три порядка превышающего диэлектрическую проницаемость вакуума, сила притяжения обкладок также увеличится в тысячу раз. В данном случае, вода может играть такую же роль в "механическом" конденсаторе, как высокопрочный диэлектрик в электрическом конденсаторе. А что касается назначения этой механической емкости, то на это можно не обращать пока никакого внимания. Каких-нибудь двести лет назад вряд ли можно было найти на этой планете ученого, который смог бы ответить, какое применение можно найти двум металлическим пластинам, а сегодня уже невозможно даже представить столь бурное развитие технического прогресса, без такого устройства как конденсатор.
Анализ выражений (7)–(23) показывает, по крайней мере на первый взгляд, полное соответствие размерностей измеряемым величинам. Теперь вернемся к известным в электромагнетизме выражениям:
(24) |
В данном случае не имеет значения, что принимается за e — э.д.с. самоиндукции или противо-э.д.с., поэтому знаки, пока, также не рассматриваются. И, если у конденсатора С имеется некоторый механический аналог Z, и если учесть, что у напряжения U (согласно (18), (21)) также имеется аналогичный параметр, равный квадрату скорости V2, то можно записать следующее выражение:
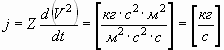 , , | (25) |
и назвать j неким механическим током, выражающим нечто, соответствующее скорости переноса масс или производительности, к примеру, переноса какой-либо жидкости по трубе. Все это, впрочем, также не играет пока принципиального значения.
Размерность индуктивности согласно (24):
(26) |
Следовательно, ее механический аналог Y будет выражен как:
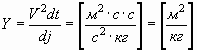 , , | (27) |
а исходное выражение будет иметь вид:
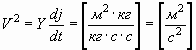 . . | (28) |
И, пользуясь методом той же аналогии, можно записать:
Теперь, имея все механические аналоги электрических величин, можно вернуться к паре сил, электрической (1) и магнитной (2):
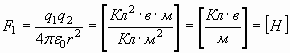 , , | (29) |
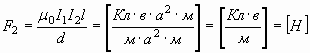 , , | (30) |
и на их основе достроить механическую пару сил (3) и (4):
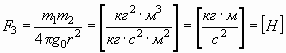 , , | (31) |
(32) |
Вычисляем размерность коэффициента пропорциональности s0:
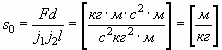 . . | (33) |
Сразу следует отметить, что ее размерность точно соответствует размерности (5) предложенной В.Л.Дятловым [2] и названной спиновой проницаемостью вакуума.
Итак, теперь мы имеем недостающую четвертую силу, не имеющую пока своего названия, позволяющую создать теперь полную симметрию в системе фундаментальных уравнений классической физики.
Закон, описывающий силовое взаимодействие двух механических токов, звучать, по-видимому, должен следующим образом: "Между двумя трубопроводами, по которым с определенной скоростью перемещается вещество с производительностями j1 и j2, имеющим длину l и находящихся на расстоянии d друг от друга, действуют равные силы взаимного притяжения (или отталкивания, в зависимости от направления переноса вещества по каждому трубопроводу), величина которых пропорциональна произведению производительностей j1 и j2 на длину трубопровода l, и обратно пропорциональна расстоянию между ними d."
Впрочем, вместо трубопроводов, может оказаться пара вытянутых масс или замкнутых колец, вращающихся в одном и том же или разных направлениях относительно некоторой системы координат.
Ввиду отсутствия ясного представления о физической природе поля, создаваемого механическим током j, назовем его пока, в соответствии с используемой временно четвертой постоянной, s-поле. Чтобы попытаться глубже понять природу этого поля, вернемся к описанию природы магнитного поля, механическим аналогом которого s-поле и является.
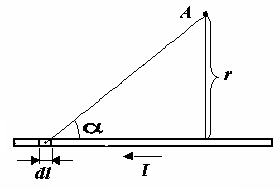 | 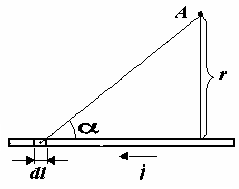 |
| а) напряженность магнитного поля | б) напряженность s-поля |
| Рис. 2 | |
Согласно рисунка 2а напряженность магнитного поля в точке А на расстоянии r от проводника с током, в скалярной форме имеет вид:
(34) |
Следовательно, напряженность s-поля в точке А, на расстоянии r от проводника с механическим током, в соответствии с рисунком 2б, будет иметь вид:
(35) |
Напряженности полей на расстоянии r от бесконечно длинного проводника с токами I и j соответственно будут равны:
(36) | |
(37) |
Здесь сразу следует отметить, что в размерности напряженности s-поля, в классической физике выражается также динамическая вязкость жидкостей и газов.
Индукция магнитного поля В и индукция s-поля Q соответственно равны:
(38) | |
(39) |
Судя по размерности, индукция s-поля может непосредственно быть связана с вращением или частотой.
И, наконец, полный поток магнитного поля Ф через поверхность S равен:
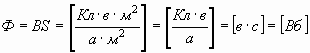 . . | (40) |
И полный поток s-поля Т, через поверхность S, соответственно:
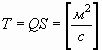 . . | (41) |
В классической физике в такой закономерности выражается также кинематическая вязкость.
Магнитный поток, создаваемый катушкой индуктивности с протекающим в ней током, равен:
(42) |
Соответственно, поток, создаваемый механической индуктивностью Y (27), с "протекающим" в нем механическим током j, будет равен:
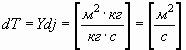 . . | (43) |
Помимо полного соответствия рассматриваемых величин их размерностям, необходимо так же обратить внимание на тот факт, что размерности емкости, индуктивности и их механических аналогов полностью присутствуют в размерностях соответствующих универсальных постоянных:
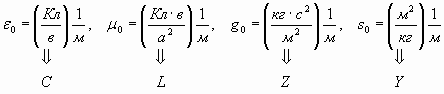 . . | (44) |
Теперь, имея полную картину сопоставлений, построим новую таблицу соответствий электрических и механических величин:
Таблица 1 | |
| Электромагнетизм | Механика |
| Закон Кулона | Закон Ньютона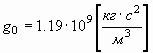 |
| Напряженность электрического поля | Напряженность гравитационного поля |
| Индукция электрического поля | Индукция гравитационного поля |
| Поток электрической индукции N = DS = [Кл] | Поток гравитационной индукции O = MS = [кг] |
| Емкость конденсатора | Емкость "механического" конденсатора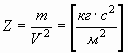 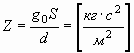 |
| Сила притяжения пластин конденсатора | Сила притяжения пластин механического конденсатора |
| Закон Ампера | Закон ... |
| Магнитная проницаемость вакуума | Спиновая проницаемость вакуума |
| Напряженность магнитного поля | Напряженность s-поля |
| Индукция магнитного поля | Индукция s-поля |
| Поток магнитного поля | Поток s-поля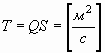 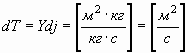 |
| Индуктивность | Механическая индуктивность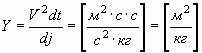 |
| Электрический ток | Механический ток |
| Электрическое напряжение U = [в] | Аналог электрического напряжения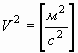 |
| Энергия W = qU = [Кл·в] = [Дж] | Энергия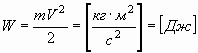 |
Если ввести понятие механической цепи, как аналога электрической цепи, то можно получить соответствующие механические активное и реактивное (емкостное и индуктивное) сопротивления. По закону Ома:
(45) |
Следовательно:
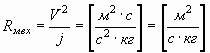 . . | (46) |
Реактивное емкостное сопротивление равно:
(47) |
откуда, реактивное сопротивление механического конденсатора:
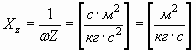 . . | (48) |
Реактивное индуктивное сопротивление равно:
(49) |
соответственно, реактивное сопротивление механической индуктивности:
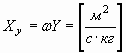 . . | (50) |
Мощность, выделяемая на активном сопротивлении:
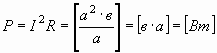 , , | (51) |
или
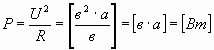 . . | (52) |
В механическом случае:
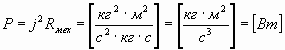 , , | (53) |
или
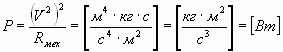 . . | (54) |
Известно, что механическая мощность определяется работой, совершаемой в единицу времени:
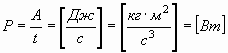 . . | (55) |
То есть, размерности полностью совпадают. Поэтому проверять дальше размерности реактивных мощностей механических цепей не имеет смысла. Можно только добавить, что произведение механического тока на "механическое" напряжение, также дает размерность мощности:
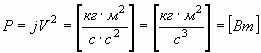 . . | (56) |
Таким образом, анализ размерностей электрических и механических величин, а также само существование гравитационного, электрического и магнитного полей, неизбежно приводят нас к выводу, что четвертое поле, названное автором временно s-полем существует! Что это за поле, торсионное, которым уже несколько лет будоражат физиков
Таблица 1 | |
| Сила электрического притяжения (или отталкивания) Диэлектрическая проницаемость вакуума Сила магнитного притяжения (или отталкивания) Магнитная проницаемость вакуума | Сила гравитационного притяжения Гравитационная проницаемость вакуума 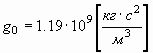 Сила действия s-поля Спиновая проницаемость вакуума |
Для подтверждения существования s-поля был проведен следующий эксперимент.
По резиновому шлангу (тонкостенному, армированному капроновой нитью, с внутренним диаметром около одного сантиметра) согнутому пополам и подвешенному в воздухе, так, чтобы трубопроводы с прямым и обратным направлением подачи воды располагались параллельно друг другу, пропускалась вода. Длинна подвешенного участка составляла три метра. Производительность, которую могли обеспечить водопроводная сеть и диаметр шланга составляла 0.4 литра в секунду. При перекрывании воды на выходе всей системы, расстояние между шлангами было равно 6 мм. При открывании вентиля, когда вода начинала бежать по системе, шланги начинали притягиваться друг к другу и при полном открывании вентиля, расстояние между шлангами было равно 2 мм. Сила притяжения приблизительно составляла 0.01 Н.
Таким образом, имея:
можно найти величину спиновой постоянной s0. Очень приближенно она равна:
(57) |
Ввиду низкого качества эксперимента и сложного характера механических напряжений шланга, погрешность измерения может значительно превышать сто процентов, но повторение опыта на других участках шланга дает устойчивый эффект притяжения близко расположенных друг к другу участков трубопроводов. Для более точного определения численного значения этого коэффициента необходимо провести более точные измерения, с производительностью значительно превышающей значение, указанное в эксперименте.
При движении воды по обоим трубопроводам в одном направлении, эффекта отталкивания зарегистрировать не удалось. Не исключено, что в механике, как и в случае с массами в законе всемирного тяготения, эффект отталкивания может иметь место только при каких-то определенных условиях.
1. Н.И. Корякин, К.Н. Быстров, П.С. Киреев. Краткий справочник по физике. — Изд. 3-е. — М.: Высшая школа, 1969. — 598 с.
2. В.Л. Дятлов. Поляризационная модель неоднородного физического вакуума. — Новосибирск: Изд-во Ин-та Математики, 1998. — 184 с.
3. Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике, кн.6. — М.: Мир, 1966. — 296 с.
4. Г.И. Шипов. Теория физического вакуума. — М.: НТ -Центр, 1993. — 362 с.
5. М.И. Кузнецов. Основы электротехники. — Изд. 7-е испр. и доп. — М.: Профтехиздат, 1960. 560 с.
6. А.Е. Акимов. Облик физики и технологии в начале ХХI века. — Верхняя Пышма: Изд-во товарищества "Диспансер", 1998. — 80 с.
7. Р.В. Поль. Учение об электричестве. — М.: Физматгиз, 1962. — 516 с.
Опубликовано:З.К. Нуриев. Недостающее звено классической механики // Наука, культура, образование
Вып. 15/16. — Горно-Алтайск; Париж, 2004. С.162-166
С момента публикации статьи "Недостающее звено классической механики" прошло уже более двух лет и автор хотел бы прокомментировать некоторые моменты, имеющие непосредственное отношение к статье и изложенным в ней идеям.
1. В самом последнем предложении следует вычеркнуть фрагмент — "как и в случае с массами". Предложение должно иметь следующий вид:
Не исключено, что в механике, в законе всемирного тяготения, эффект отталкивания может иметь место только при каких-то определенных условиях.
2. Необходимо отдельно остановиться на некоторых моментах, часто вызывающих вопросы.
В частности, под вытянутыми массами можно понимать не что иное, как массы вытянутые в линию, виде той же проволоки, например. Примером взаимодействия двух вытянутых масс может служить движение двух железнодорожных составов, движущихся в одном или противоположных направлениях. С другой стороны, любое кольцо также является вытянутой массой, конец которой соединен с началом по траектории с конкретным радиусом.
Что касается стекол, смоченных изнутри или находящихся в воде, которые трудно разъединить, то автор высказал только еще одну возможную причину такого притяжения. Современная физика объясняет этот эффект либо электростатической природой взаимодействия, либо, в крайнем случае, необходимостью заполнения межплоскостного пространства водой. Иначе говоря, необходимо какое-то время, чтобы вода заполнила межплоскостное пространство при ограниченном сечении, через которое вода должна это пространство заполнить. То есть, если стекла разводить очень медленно, то и силы, удерживающие их вместе, не проявятся. Почему, тогда в случае со смоченными изнутри стеклами, при разъединении последних, вода не перемещается к центру или к тем граням, которые до конца могут оставаться соприкасающимися друг к другу.
Теперь, если в случае со стеклами, электростатические силы могут влиять на притяжение их друг к другу, как тогда объяснить природу сил, удерживающих вместе две металлические пластины, смоченные сильно соленой водой? Ведь электрические зарядовые связи в таком случае становятся нейтральными, а пластины разъединить все равно трудно.
Силы межмолекулярного взаимодействия двух однородных тел, которые также могут оказывать влияние, в данном случае, не существенны, так как сухие стекла или металлические пластины разъединяются значительно легче.
3. Теперь относительно эксперимента. Продолжительные попытки оценить количественные характеристики спинового поля приводят автора к мысли, что, скорее всего, прав В.Л.Дятлов. Реальное значение спиновой проницаемости вакуума составляет 0.9·10-26[м·кг-1]. В эксперименте, вероятнее всего, были зарегистрированы какие-то механические деформации самого шланга. Зарегистрировать действие спинового поля при таком значении спиновой проницаемости вакуума, является достаточно трудной задачей. Для решения ее нужна какая-то неординарная идея или очень большие энергии для проявления силового действия спинового поля.
Автор пытался зарегистрировать действие этого поля при прохождении около эталонного груза, подвешенного на неподвижной опоре, железнодорожного состава. Груженый состав может обеспечивать "механический" ток порядка нескольких десятков тонн в секунду. При таком "токе", даже при значении спиновой проницаемости вакуума, вычисленной Дятловым, можно зарегистрировать реакцию груза подвешенного на нити к неподвижной опоре. А по углу отклонения груза можно вычислить и энергию импульса, вызвавшего колебание. Однако, как оказалось, даже такой эксперимент требует очень серьезной подготовки. Для этого должны быть учтены следующие факты:
Во-первых, силовое воздействие вихревых воздушных потоков на много порядков превышает силовое воздействие измеряемого поля, поэтому маятник должен исключать воздействие этих потоков, то есть, должен быть заключен в какой-то короб.
Во-вторых, земля, вблизи ж/д полотна, при прохождении по нему груженого состава, начинает содрогаться и сотрясает все, что находится близко к полотну. А напряженность спинового поля тем выше, чем ближе рассматриваемая точка расположена к "механическому" току.
В-третьих, материал, из которого необходимо делать коробку для маятника, должен быть "прозрачным" для спинового поля, то есть, не должен его шунтировать. А об отношении материалов к спиновому полю, мы, пока, вообще ничего не знаем.
В качестве лирического отступления можно вспомнить небольшой инцидент, связанный именно с такими измерениями. Дело было как раз после очередного теракта на железной дороге. Все люди, работающие в этой сфере, видимо, были специально дополнительно проинформированы на этот счет и внимательно следили за всем, что имеет отношение к железной дороге. Видимо, кто-то из бдительных машинистов, проезжая мимо человека, стоящего очень близко к полотну и внимательно за чем-то наблюдающего, сообщил об этом "куда надо" и руководство не нашло ничего лучше, как отправить на это место работавшую в нескольких километрах бригаду ремонтников. Завидев вдалеке оранжевые точки, автор данных строк на всякий случай подался в кусты. Дойдя до моего датчика, который к счастью оказался незамеченным, они рассредоточились и начали искать подозрительного типа. Минут через пять кто-то крикнул, что "он" видимо убежал, и они пошли обратно. Продолжить эксперименты удалось после того, когда оранжевые точки уже нельзя было разглядеть на горизонте.
4. Вопрос регистрации и измерения спинового поля остается открытым. Попытки автора каким-либо образом замерить это поле результатов пока не принесли и являются объектом дальнейших исследований. Вячеслав Лукич Дятлов, достаточно подробно рассмотревший природу спинового поля через силу "Лоренца" (хотя, по праву, она должна называться теперь — сила Дятлова) в своей книге "Поляризационная модель неоднородного физического вакуума", вышедшей еще в 1998 году, уделял экспериментальной части самое большое внимание.
Последние несколько личных встреч с Вячеславом Лукичом были посвящены исключительно обсуждению принципов, на которых можно строить измерительные приборы такого класса. По его идеям было изготовлено несколько типов датчиков для попытки регистрации и измерения как самого спинового поля, так и регистрации изменения электрических и магнитных величин от меняющихся характеристик самого физического вакуума, так как вопрос выявления пространственных неоднородностей являлся одной из основных тем, которой он занимался последние годы. Однако, этим приборам, выполненным большей частью в кустарных условиях, не хватало ни чувствительности, ни каких либо известных способов снятия информации с некоторых типов датчиков. Например, необходимо было непрерывно (в режиме реального времени, в течение нескольких месяцев) измерять небольшие угловые отклонения датчика, которые реагировали на крутящий момент, примерно 10-6...10-7 Нм (а возможно и значительно меньше). Любой датчик угла конденсаторного типа, используемый для измерения поворота основного датчика, даже при токах всего в несколько микроампер, "втягивал" емкость на максимальную площадь перекрытия секторов и надолго "залипал" в этом состоянии. Для изготовления многосекторных датчиков с компенсацией зарядовой связи требовалась очень высокая механическая точность, чего в кустарных условиях мы добиться никак не могли.
Измерители угловых отклонений, построенные на базе оптоэлектронной пары, не могли мерить маленькие углы отклонения и сильно зависели от температуры, стабилизация или компенсация которой так же требовали создания дополнительных высокоточных электронных узлов.
Пришлось остановиться на оптическом датчике, выполненном на базе обыкновенной китайской лазерной указки, которую можно купить в любом киоске. При отводе шкалы регистрации на три метра от рабочего зеркала, такой датчик позволял мерить углы до десятых долей градуса, но тоже имел один большой недостаток. Необходимо было "сидеть" около этого датчика и каждый час, как минимум, записывать показания. Реально снимать показания удавалось в сумме не более 6...7 часов в сутки, а такие "рваные" данные не позволяли обнаружить какую либо закономерность с фазовыми состояниями планет солнечной системы, луны или какими-то другими явлениями земного или неземного происхождения.
5. Интересной иллюстрацией действия спинового поля, является эксперимент проведенный Хайрулиным Ильфиром Фидаевичем. Подробное описание конструкции установки, можно найти у него на сайте: http://ilfir.narod.ru/chronos/index1.htm.
Вкратце, суть эксперимента заключается в том, что в центрифугу, закрытую кожухом для исключения вихревых потоков воздуха опускался свинцовый груз, подвешенный на одном конце горизонтально расположенной алюминиевой трубки с противовесом на другом конце. Вся эта конструкция также подвешивалась на нити. Груз оставался неподвижным, пока центрифуга находилась в состоянии неподвижности. Как только центрифуга начинала раскручиваться, груз приходил в движение по (или против) часовой, пока это движение не ограничивалось внутренней стенкой кожуха самой центрифуги. Приведено несколько графиков зависимости направления движения груза от направления вращения центрифуги, первоначальной ориентации горизонтальной трубки, времени суток и т. д. Автор этого эксперимента пытался подвести физику этого эффекта под свою гравитационную модель, однако, после того, как удалось с ним связаться и показать свое видение физики этого явления, он проявил интерес к новому объяснению причин движения груза при вращающейся центрифуге и даже выставил на какое-то время статью "Недостающее звено классической механики" на своем сайте.
Хайрулин И.Ф. заострил внимание на направлении вращения центрифуги, в то время, как основной причиной появления силы, действующей на груз, является не само вращение а разгон и остановка центрифуги. По аналогии с катушкой индуктивности, если электрический заряд поместить в катушку с постоянно протекающим в ней током, то на заряд никакая сила действовать не будет. Но стоит только разорвать электрическую цепь, то в сам момент спадания тока в катушке, приращение магнитного поля окажет силовое воздействие на заряд. То же самое происходит и при подключении катушки к источнику постоянного напряжения, только направление вектора силы в этом случае меняет знак на противоположный. Так же и в эксперименте Хайрулина, сила действовала на груз только в момент разгона центрифуги и груз продолжал свое движение уже по инерции. Если груз удерживать от движения до полного разгона центрифуги, то сам он уже двигаться не будет и при отключении центрифуги, груз должен начать движение в противоположном направлении (от того направления, которое он должен иметь при разгоне)
К сожалению, на момент установления связи с Хайрулиным, установки с центрифугой у него уже не было, и проверить все это уже не было возможности.
В соответствии со всем вышеизложенным, автор будет рад любым идеям, связанным с измерением сверхслабых (по углу и по моменту) угловых отклонений, способами регистрации спинового поля или новым объяснением уже каких-то известных явлений.
Вопросы и предложения можно отправлять по адресу: znuriev @ rambler. ru